Компьютеры и Интернет
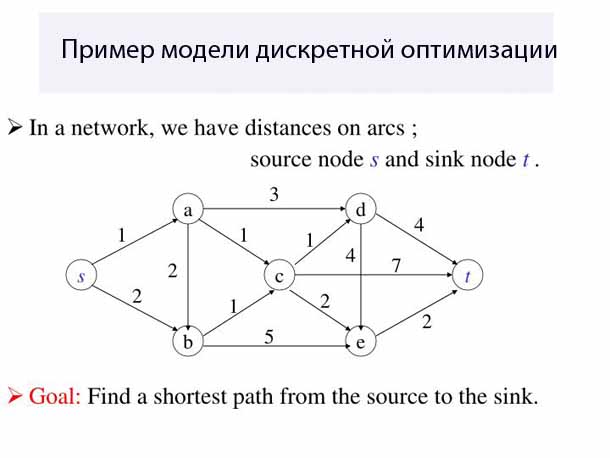
Дискретная оптимизация – категория оптимизации, концепция которой используется в области компьютерных наук и математики. В отличие от конкретной или непрерывной оптимизации, дискретная оптимизация использует только целые числа, а не дроби, чтобы выполнить максимизацию функций, что и является целью всей оптимизации. В дальнейшем есть возможность разделить дискретную оптимизацию в целочисленное программирование и комбинаторную оптимизацию.
Непрерывная оптимизация относится к максимизации функций с непрерывными, реальными цифрами, начиная от набора целых чисел и всеми значения, которые лежат между ними. Это означает, что численные значения которые используются могут представлять любое значение, которое может проявляться как в реальном физическом мире так и в абстрактном мире математики. Отрицательные числа, а также дроби и десятичные, которые работают на неопределенный срок. Эта форма оптимизации является наиболее сложной, и она принимает наиболее точный подход к математической функции.
Другая ветвь дискретной оптимизации, в целом, это движущая цель оптимизации и она остаётся прежней — максимизировать результаты математических функций, так как они применяются в вычислительной технике или других областях. В отличие от своего аналога непрерывной оптимизации, этот тип оптимизации имеет дело только с дискретными численными значениями. Это конкретные числа, например, число 2 или 647. В то время как другая ветвь проходит вдоль линии, этой дискретной ветке не хватает плавных переходов от одного целого числа к другому — фракции, которые лежат между ними не в счёт.
Как и в области самой оптимизации, дискретную оптимизацию можно разделить на две категории: целочисленное программирование и комбинаторная оптимизация. В области компьютерных наук, целочисленные переменные пределы программирования находятся в программе в целых числах, то есть дроби и отрицательные числа запрещены в программе. Комбинаторная оптимизация используется в компьютерных науках, а также в области математики, и она довольно сложная. Она предполагает интеграцию операций оптимизации и решения в разных видах графики. Из-за конечного и конкретного характера дискретных числовых значений, графики не гладкие, а наоборот, подчеркивают различия на вертикальных и горизонтальных осях, которые появляются между двумя значениями.
Где и как используется непрерывная или дискретная оптимизация – это зависит исключительно от области и целей конкретного проекта. Помимо математики и компьютерных приложений, в области машиностроения, экономики, или механических наук, могут быть использованы различные виды оптимизации. Согласно проекту, это может быть, ни дискретная, ни непрерывная оптимизация — их только две и в других категориях оптимизации.
